Sprint Profiling – Common Problems and Solutions Part 1
Introduction
Short sprints (i.e., sprints without deceleration, usually <6sec) profiling represents a process of fitting a simple mathematical model (mono-exponential model – explained later) to the observed data with the aims of describing/summarizing, comparing, predicting, and hopefully making some intervention/causal claims. Process of model fitting, or in this case profiling, is an optimization process of finding the model parameters that best fit the data (i.e., minimize the error, most often the sum of squared errors, although other errors can be minimized). In plain English, we are making a simple (but useful) map (i.e., model) of the territory using collected data.
In this article I will guide you through common ways of making a map (i.e., profiling) from different types of short sprint data. This includes, but it is not limited to: (1) radar gun or laser gun data, (2) tether data (like DynaSpeed), (3) timing gates or photo cells data, and (4) GPS (like Catapult) or local positioning systems (LPS; like Kinexon) used to monitor the training sessions. All of these have some specific problems that can lead to biased and imprecise maps. I will walk you through common scenarios that you will stumble upon and provide some potential solutions that can alleviate certain problems.
We are going to do the analysis in R language (I wholeheartedly recommend installing RStudio from Posit) using the {shorts} package which you can install by running:
# Install from CRAN
install.packages("shorts")
# Or the development version from GitHub
# install.packages("remotes")
remotes::install_github("mladenjovanovic/shorts")I recommend installing {shorts} package from GitHub, since here you can find the latest developmental version. I must note that for the code in this article to run, you will need 2.5.0.9000+ version of the {shorts} package, which is still not on CRAN by the time of this writing.
I will provide the R code for everything, and if the code is not shown just click the “Show/Hide Code” which is located over the figure or table output.
The Map
Sprint kinematics can be simply mapped-out using the mono-exponential Equation 1.
\[
v(t) = MSS \times (1 – e^{-\frac{t}{TAU}})
\tag{1}\]
The parameters in Equation 1 are the Maximum Sprinting Speed (\(MSS\)), which is measured in meters per second (\(ms^{-1}\)), and the Relative Acceleration (\(TAU\)), which is measured in seconds (\(s\)). The parameter \(TAU\) denotes the quotient obtained by dividing the \(MSS\) by the initial Maximum Acceleration (\(MAC\)), which is expressed in units of meters per second squared (\(ms^{-2}\)) and can be represented by Equation 2. It should be noted that \(TAU\) represents the duration needed to attain a velocity equivalent to 63.2% of the \(MSS\), as determined by the given Equation 1.
\[
MAC = \frac{MSS}{TAU}
\tag{2}\]
While \(TAU\) is a parameter employed in the equations and subsequently estimated, it is advisable to employ and report \(MAC\) as it is more straightforward to comprehend, particularly for professionals and trainers.
Having said that, the another form of Equation 1 that can be used as an alternative is Equation 3 in which we changed \(TAU\) for \(\frac{MSS}{TAU}\).
\[
v(t) = MSS \times (1 – e^{-\frac{t \times MAC}{MSS}})
\tag{3}\]
By performing derivation of Equation 1, we get equation for the horizontal equation (Equation 4).
\[
a(t) = \frac{MSS}{TAU} \times e^{-\frac{t}{}}
\tag{4}\]
The equation for distance covered (Equation 5) can be derived by integrating Equation 1.
\[
d(t) = MSS \times (t + TAU \times e^{-\frac{t}{TAU}}) – MSS \times TAU
\tag{5}\]
One cool feature of the mono-exponential model is the linear relationship between acceleration and velocity, making it great for profiling purposes (Equation 6).
\[
a(v) = MAC – v \times \frac{MAC}{MSS}
\tag{6}\]
All of this is easier to describe graphically. Figure 1 depicts mathematical model behavior using true parameter values for four athletes.
Show/Hide Code
library(tidyverse)
library(shorts)
kinematics_df <- tribble(
~athlete, ~MSS, ~MAC,
"A (high speed, low acceleration)", 10, 6,
"B (low speed, high acceleration)", 7, 9,
"C (low speed, low acceleration)", 7, 6,
"D (high speed, high acceleration)", 10, 9
) %>%
group_by(athlete) %>%
reframe(predict_kinematics(MSS = MSS, MAC = MAC, max_time = 20, frequency = 10)) %>%
ungroup()
# Time velocity
gg1 <- kinematics_df %>%
filter(time <= 10) %>%
ggplot(aes(x = time, y = velocity, color = athlete)) +
geom_line() +
xlab("Time (s)") +
ylab("Velocity (m/s)") +
theme(legend.position = c(0.6, 0.4)) +
scale_x_continuous(expand = c(0, 0), limits = c(0, NA)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
gg1
# Distance velocity
gg2 <- kinematics_df %>%
filter(distance <= 50) %>%
ggplot(aes(x = distance, y = velocity, color = athlete)) +
geom_line() +
xlab("Distance (m)") +
ylab("Velocity (m/s)") +
theme(legend.position = c(0.6, 0.4)) +
scale_x_continuous(expand = c(0, 0), limits = c(0, NA)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
gg2
# Acceleration - time
gg3 <- kinematics_df %>%
filter(time <= 10) %>%
ggplot(aes(x = time, y = acceleration, color = athlete)) +
geom_line() +
xlab("Time (s)") +
ylab("Acceleration (m/s/s)") +
theme(legend.position = c(0.6, 0.4)) +
scale_x_continuous(expand = c(0, 0), limits = c(0, NA)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
gg3
# Acceleration - distance
gg4 <- kinematics_df %>%
filter(distance <= 50) %>%
ggplot(aes(x = distance, y = acceleration, color = athlete)) +
geom_line() +
xlab("Distance (m)") +
ylab("Acceleration (m/s/s)") +
theme(legend.position = c(0.6, 0.4)) +
scale_x_continuous(expand = c(0, 0), limits = c(0, NA)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
gg4
# Distance - time
gg5 <- kinematics_df %>%
filter(distance <= 50) %>%
ggplot(aes(x = distance, y = time, color = athlete)) +
geom_line() +
xlab("Distance (m)") +
ylab("Time (s)") +
theme(legend.position = c(0.8, 0.3)) +
scale_x_continuous(expand = c(0, 0), limits = c(0, NA)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
gg5
gg6 <- kinematics_df %>%
ggplot(aes(x = velocity, y = acceleration, color = athlete)) +
geom_line() +
xlab("Velocity (m/s)") +
ylab("Acceleration (m/s/s)") +
theme(legend.position = c(0.7, 0.8)) +
scale_x_continuous(expand = c(0, 0), limits = c(0, NA)) +
scale_y_continuous(expand = c(0, 0), limits = c(0, NA))
gg6
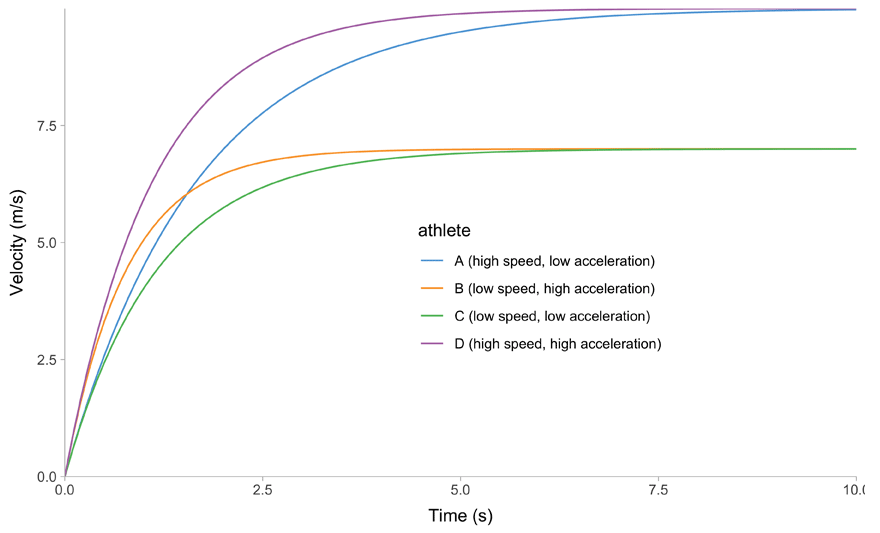
(a) Time~Velocity trace
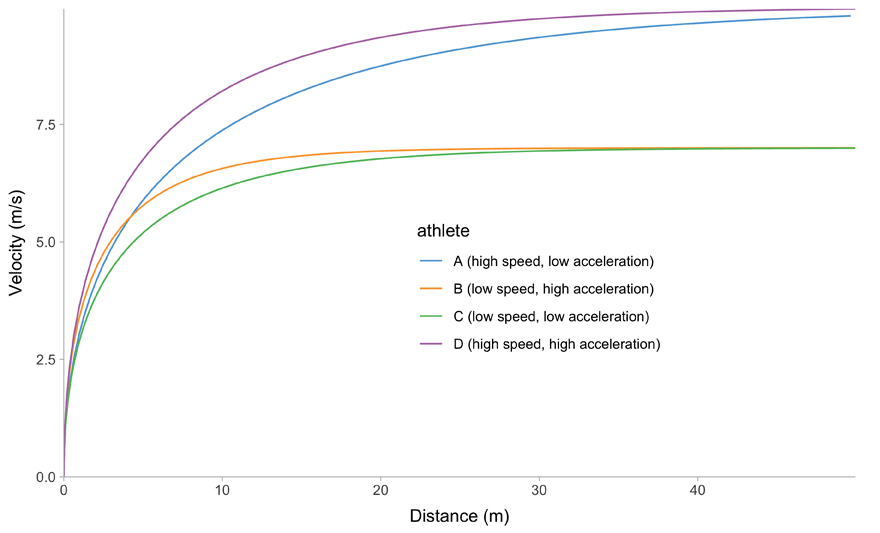
(b) Distance~Velocity trace
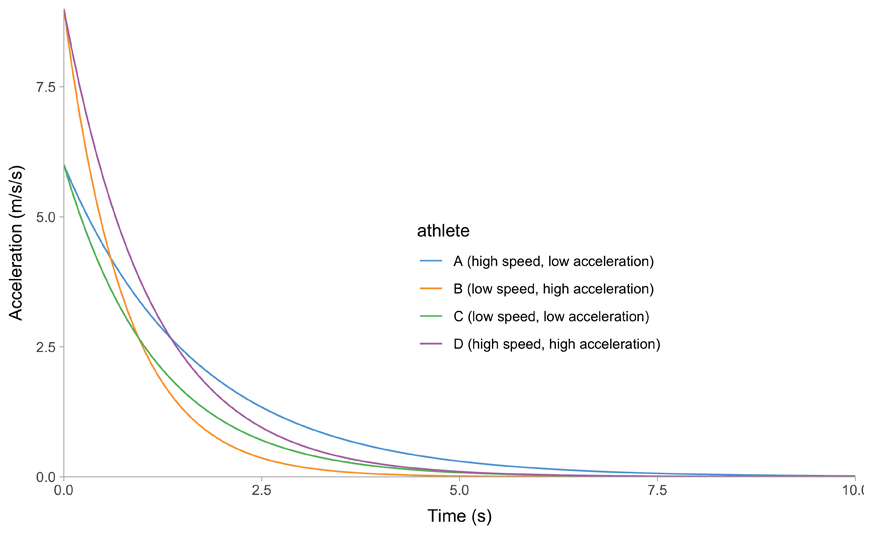
(c) Time~Acceleration trace
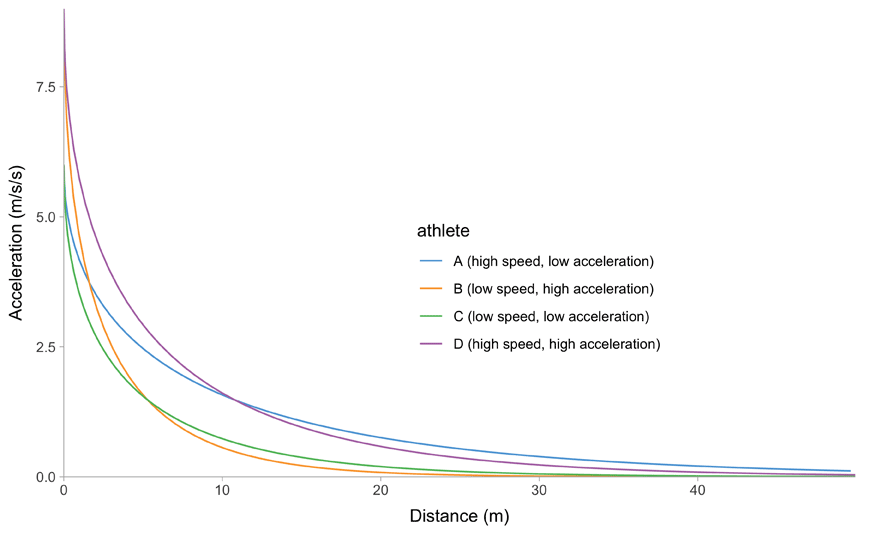
(d) Distance~Acceleration trace
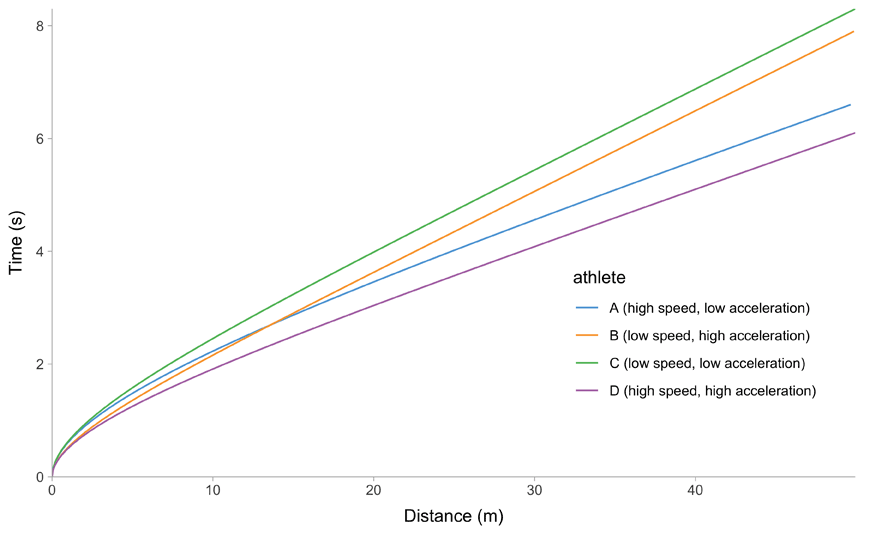
(e) Distace~Time trace
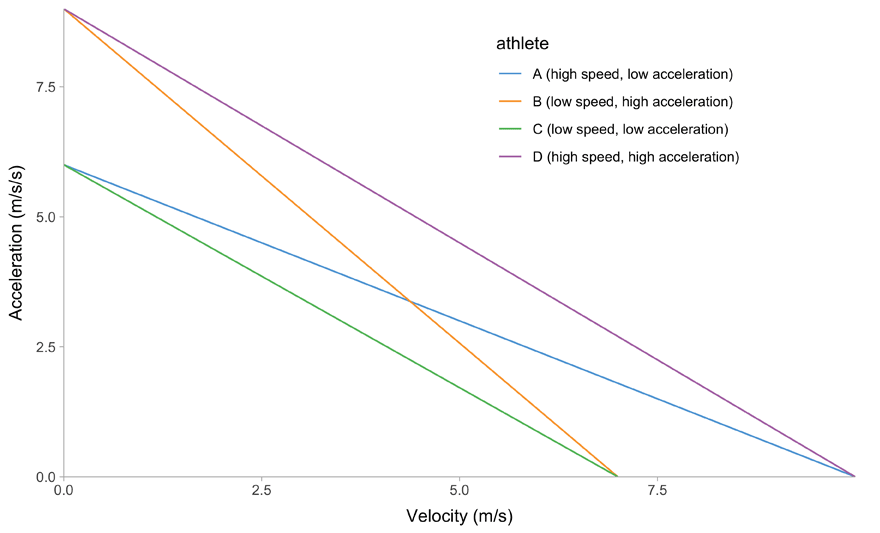
(f) Velocity~Acceleration trace
Figure 1: Kinematics of the mono-exponential model using four hypothetical athletes
Once we have the model parameters, we can estimate (i.e., predict) various model kinematic behavior. If we know the weight and height of the athlete, as well as air conditions (pressure, temperature, and wind), we can add into the mix another model to calculate air resistance and get kinetics, or forces, power, and work values. With forces being known, we can estimate Force-Velocity Profile (FVP). This is a topic for another article. In this one we will stick to the simple mono-exponential model and \(MSS\) and \(MAC\) parameters, since if we cannot estimate them correctly, we will propagate the errors to all other predictions which depend on their valid and precise estimation. In plain English again, if you suck at estimating \(MAC\) or \(MSS\), then the FVP will be shit as well. So let us focus on this task first, and worry about fancy FVP later (or in another article).
Due to it’s elegant linear relationship between acceleration and velocity (Figure 1 (f)), we can also call mono-exponential model a Acceleration-Velocity Profile, or AVP. So, when we estimate the AVP, we estimate the \(MSS\) and \(MAC\) parameters using the mono-exponential model.
Why is this better than looking at the raw data?
My Devil’s advocate nature motivates me that in a room full of coaches, I will defend “theory and sports science” (I will defend the nerds), and in the room full of “evidence-based lab-coats”, I will defend practice and coaches (I will defend the jocks). So let me clearly state that this…










Responses