Exploring Architectural Gearing: The Dynamic Engine Behind Muscle Performance

Muscles are complex, highly specialized structures that play a critical role in human movement and function. The architecture of a muscle, which includes its thickness, fascicle length, and pennation angle, is fundamental to understanding how muscles generate force and facilitate movement. In this blog, I will delve into the relationship between muscle architecture and performance, with a particular focus on the concept of architectural gearing. I will explore how muscle shape changes during contraction, how these changes affect pennation angle, and ultimately how this change in pennation angle (architectural gearing) can enhance muscle performance by optimizing force production and shortening velocity. First, however, let’s start with some background.

Muscle Architecture: The Foundation of Force and Movement

Muscle architecture refers to the arrangement of muscle fibers within a muscle and is one of the primary determinants of a muscle’s mechanical function. Key architectural parameters include muscle thickness, fascicle length, and pennation angle.

• Muscle Thickness: This refers to the size of a muscle. A thicker muscle typically has a greater number of muscle fibers in parallel, which increases its potential to generate force.
• Fascicle Length: Fascicles are bundles of muscle fibers, and their length is a key determinant of a muscle’s capacity for shortening. Longer fascicles can shorten faster and produce more force at a given shortening velocity.
• Pennation Angle: The pennation angle is the angle between the muscle fibers and the line of action of the muscle. Muscles with a greater pennation angle can pack more fibers into a given volume, which can increase the force generated by the muscle, albeit at the cost of reduced shortening velocity.

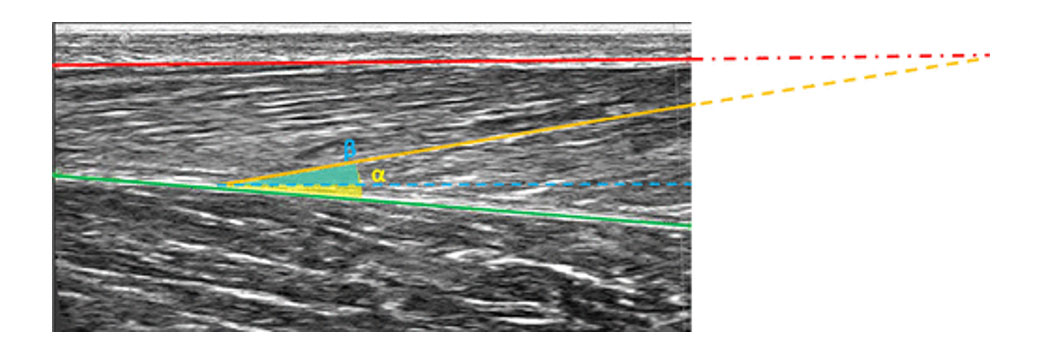
Figure 1: Diagram showing muscle structure including fascicle arrangement, muscle thickness, and pennation angle in a B-mode ultrasound image of the gastrocnemius medialis.

Figure 1: The red and green lines depict the superficial and deep aponeurosis, respectively, while the orange line depicts a fascicle. The vertical distance between the red and green lines represents the muscle thickness. The dashed red and orange lines represent the linearly extrapolated superficial aponeurosis and muscle fascicle, respectively. The pennation angle is often computed as the angle between the deep aponeurosis and fascicle (α, yellow). In scientific paper, however, the angle of the fascicle is often determined relative to the horizontal bottom of the image, here, illustrated with the blue dashed line (β, blue). Figure adopted from [1].

The Interplay Between Fascicle Length, Pennation Angle, and Muscle Performance

The relationship between fascicle length, pennation angle, and muscle performance is complex. Fascicle length is directly related to the muscle’s maximum shortening velocity. Longer fascicles can shorten more rapidly, thereby contributing to faster muscle contraction and higher joint angular velocities.

Pennation angle, on the other hand, is associated with the muscle’s maximum force-generating capacity. A greater pennation angle allows more fibers to fit into the muscle, thereby increasing the force it can generate. However, this arrangement comes at the cost of reduced shortening velocity since the fibers are aligned at an angle rather than parallel to the direction of force generation (Figure 2).

Specifically, the schematic in Figure 2 assumes that the angle of pennation (Ɵ) is 30° in the pennate muscle (the assertion applies to any angle). The volume of both muscles is 40 arbitrary units (AU), where the depth is 1 AU. The thickness of the pennate muscle is 4 AU and the length of the aponeurosis with fibres attached is 10 AU. The fascicle length (Lf) of the parallel muscle is 16 AU and the thickness (and, in this case, the physiological cross-sectional area, PCSA), is 2.5 AU.

To calculate the PCSA of the pennate muscle we first calculate Lfas: (muscle thickness) 4AU / sin30°=8AU. The PCSA of the pennate muscle is subsequently calculated as muscle volume/Lf: 40AU/8AU=5AU. For the calculation of force and velocity of the muscle we assume that the force-velocity characteristics of the fibres are the same in both muscles.

The tendon forces of the pennate and parallel muscles are as follows:

Pennate: 5AU * cos30°=4.33 AU

Parallel: 2.5AU * cos0°=2.5AU

Therefore, the pennate muscle produces 1.73 x (4.33/2.5) as much force as the parallel muscle.

However, with regard to the shortening velocity the following applies:

Pennate: 8AU * cos30°=6.93AU

Parallel: 16AU * cos0°=16AU

Therefore, the pennate muscle shortens at 0.43 x (6.93/16) the velocity of the parallel muscle. Multiplying these two factors (0.43x 1.73) shows that the pennate muscle in this example produces only 74% of the power of a parallel muscle of the same volume (assuming no change in pennation angle upon contraction).

Thus, there is a trade-off between force and velocity depending on the muscle’s architectural characteristics. Muscles optimized for force generation (e.g., the quadriceps) typically have a greater pennation angle, while muscles optimized for speed (e.g., the sartorius) have longer fascicles and a smaller pennation angle.

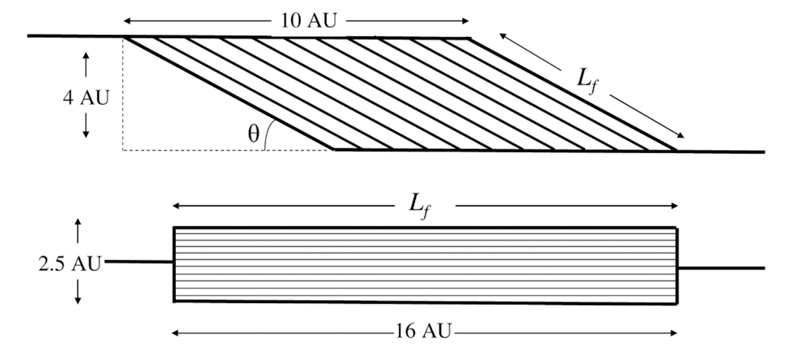
Figure 2: Diagram showing how a pennate muscle produces less power than a parallel-fibred muscle of the same volume. Adopted from [2].

Muscle Shape Changes During Contraction

The discussion so far has largely assumed that the muscles retain their resting shape during contraction. When a muscle contracts, its shape however changes: the fascicles shorten and bulge in the thickness direction. This bulging will cause a lateral force to be exerted onto neighbouring fascicles, in turn forcing the whole muscle to also expand in the thickness direction. As a result, fascicles rotate about their insertion point at the aponeurosis/tendon, in turn increasing their angle relative to the aponeurosis and increasing whole-muscle thickness while inducing longitudinal muscle shortening (Video 1, Figure 3). Fascicle rotation (i.e., the change in pennation angle) thereby contributes directly to the overall muscle length change (and hence contraction velocity) in addition to that caused by changes in length of the fascicles themselves.

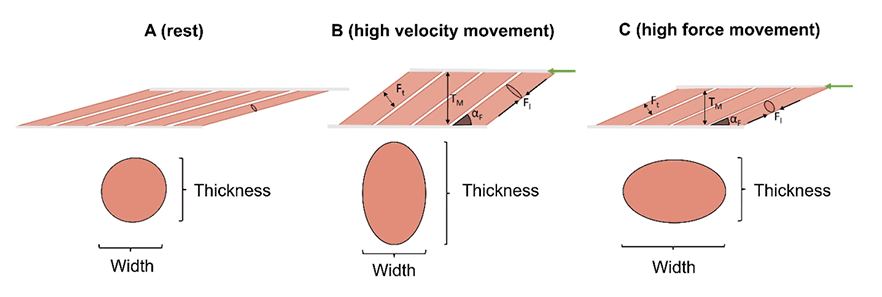
Figure 3: (A) Schematic illustration of muscle fascicles in a resting muscle before contraction. (B, C) Concentric muscle contraction causing whole-muscle bulging in the thickness and width directions, respectively.

Figure 3: Due to the close packing of fascicles and the shallow fascicle angle at rest (A), there is insufficient space for fascicle bulging. Due to this insufficient space, any fascicle bulging in the thickness direction will force the fascicles to rotate to greater angles (largerαF), as this will increase space between the fascicles. This rotation also increases whole-muscle thickness (TM). (C) During high-force contractions (i.e., when external loads are high), fascicles produce a high force. The longitudinal force exerted by the fascicles (FL) acts against whole-muscle bulging in the thickness direction. Therefore, fascicle and whole-muscle bulging must predominately occur in the width direction (see cross-sections in C). The reduced muscle thickening limits fascicle rotation and contributes to slower whole-muscle shortening (muscle shortening speed is similar to fascicle shortening speeds) (green arrow). However, because the fascicles remain more closely aligned with the direction of whole-muscle shortening, a greater proportion of the fascicle force is directed along the tendon, therefore whole-muscle maximum force is greatest. In contrast, when the fascicles have to produce force rapidly, they cannot produce a lot of force. Therefore, the rapid shortening still increases the thickness of the fascicles and in turn whole muscle, with less force acting to reduce whole muscle thickness. The result is that the faster rotation of the fascicles increases whole muscle velocity, thus increasing muscle shortening velocity. The force produced by fascicles therefore determines whether the operates more favourably for high force production or high shortening velocities. This variable gearing capacity, based on muscle forces, allows for increased muscle shortening speeds under low-force contractions (when fascicle rotation is great) yet increases effective (projected) muscle force generation during high load contractions (when fascicle rotation is reduced). Thus, pennate muscles can intrinsically change gears to optimize contractile capacity as the force requirements of a task are changed. Adopted from [3].

Architectural Gearing: Enhancing Muscle Performance

As a result of the changes in pennation angle during contraction, the overall muscle shortening velocity is therefore often higher than the fascicle shortening velocity. Indeed, architectural gearing refers to /is calculated as the ratio between overall muscle and muscle fascicle shortening (or lengthening) velocity and it often >1.0 in various contraction conditions, meaning that the muscle shortens faster than the fascicles [3]. For example, if the muscle shortening velocity is 1.5 mm/s, and the fascicle shortening velocity 1 mm/s, the architectural gearing ration is 1.5/1 = 1.5, thus indicating a greater muscle shortening velocity than fascicle shortening velocity.

In addition to increasing overall shortening speed, architectural gearing also allows the muscle to increase its force production as fascicles function at a slower shortening velocity than the whole muscle. Architectural gearing thus offers several advantages: